Befasst man sich mit maschinellem Lernen, dann kommt man an Deep Learning nicht vorbei, denn Neural Networks liefern erstaunliche Ergebnisse in verschiedensten Bereichen. Die Hürde für Entwickler sie einzusetzen ist aufgrund von Bibliotheken wie z.B. Tensorflow oder Theano relativ gering, da sie Großteile der Grundlagen verstecken. Dies gilt auch für Backpropagation, obwohl es sich dabei um die Schlüsseltechnologie des Lernens in Multilayer Neural Networks handelt.
Warum Backpropagation?
Neural Networks mit nur einem Layer stießen schnell an ihre Grenzen in punkto Komplexität. Durch die Aneinanderreihung von mehrerer Layer war es möglich, kompliziertere Funktionen zu modellieren. Doch damit wurde auch der Lernprozess schwieriger. Denn, wie der Input, durchläuft auch die Optimierung der Gewichte nun die Layer sequenziell nacheinander. Dies ist ein entscheidender Unterschied, da es die Optimierung des 1. Layers abhängig vom 2. Layer macht, und diesen wiederum vom 3. Layer usw. Dieses mathematische Problem löst die Backpropagation und macht sie somit unabdingbar für den Lernprozess in Neuronalen Netzen.
Wir möchten in diesem Blogbeitrag auf die grundlegende Idee dahinter eingehen und graphisch veranschaulichen, bevor du dich der Mathematik, *Räusper* dem Formelwirrwarr, widmest. Der Beitrag basiert auf dem grundlegenden Wissen über die Funktionsweise eines künstlichen Neurons. Der Wikipedia Artikel hilft dir dabei, dir dieses Wissen wieder ins Gedächtnis zu rufen.
Backpropagation Intuition
Um das Prinzip der Backpropagation zu verstehen, fängt man am besten damit an sich vorzustellen, in welcher Weise sich das Ergebnis des Netzes ändern soll, um der Groundtruth näher zu kommen. Betrachten wir dies an dem weitverbreiteten MNIST Beispiel in Abbildung 1. Es handelt sich dabei um eine große Datenbank mit handgeschriebenen Ziffern, die als 28×28 Pixel große Bilder abgespeichert sind.
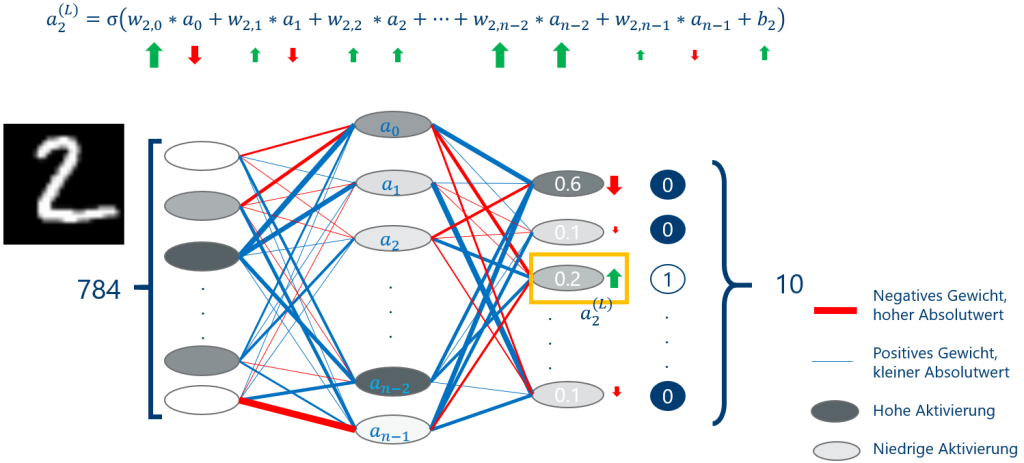
Was ist unser Ziel?
Unser Ziel ist es, die Zahl auf dem Input-Bild automatisch zu erkennen. Hierfür gibt es in dem letzten Layer 10 Neuronen für die jeweiligen Zahlen 0 bis 9. Für den Input der geschriebenen “2” hat in diesem untrainierten Netz das zugehörige Neuron für den Wert 2 am Ende eine niedrige Aktivierung von 0.2. Dieser Wert ergibt sich durch die gewichtete Summe seiner Eingaben plus einen sogenannten Bias, die in eine Aktivierungsfunktion gesteckt wird. Wir möchten erreichen, dass sich die Aktivierung stark nach oben verändert, während die Werte der anderen Neuronen kleiner werden sollen. Dies gilt vor allem für das Neuron 0, da der Wert hier bei 0.6 liegt. Der Abstand zum richtigen Wert 0 ist damit viel größer als z.B. beim Neuron 1 (0.1).
Anpassung der Variablen!
Dementsprechend müssen auch die Variablen, von denen das Ergebnis abhängt, unterschiedlich stark verändert werden. In Abbildung 1 können wir sehen, wie sich die Variablen mit direktem Einfluss auf das Neuron 2 verändern sollten. Wenn wir davon ausgehen, dass alle Aktivierungen positiv sind, können wir daraus schließen, dass die Gewichte alle größer werden müssen. Bei den Aktivierungen der Hidden Layer hängt dies dagegen davon ab, ob das zugehörige Gewicht positiv oder negativ ist. Wenn es negativ ist, muss die Aktivierung kleiner werden. Eine wichtige Feststellung ist außerdem, dass eine kleine Änderung beim Gewicht einen umso größeren Einfluss auf das Ergebnis hat, je größer die Aktivierung ist und umgekehrt. Das sehen wir in Abbildung 1 an den Pfeilstärken, wenn wir an-2 und an-1 miteinander vergleichen.
Die Aktivierungen haben zudem auch Einfluss auf alle anderen Neuronen des Output Layers, also nicht nur auf das Ergebnis für die Zahl 2, sondern auch für 0 bis 9. Wenn wir diese Neuronen einzeln betrachten, haben alle eine eigene Vorstellung davon, in welche Richtung und wie stark sich die Aktivierungen bewegen sollten. Ein Kompromiss muss her, deswegen berechnen wir den Durchschnitt.
Und Backpropagation?
Die Aktivierungen in der versteckten Schicht sind keine Parameter im Netzwerk, die direkt veränderbar sind. Sie hängen wieder von den Eingabedaten und Gewichten der vorherigen Layer ab. Wir können diese jedoch genauso behandeln wie zuvor die Output Layer. Das zu lösende Problem hat sich einen Layer weiter nach vorne verschoben, wie in Abbildung 2 dargestellt. Backpropagation ist deswegen ein rekursiver Ansatz, mit dem Input Layer als Abbruchkriterium. In diesem Fall haben wir die Änderungen für alle Parameter bestimmt, zumindest was dieses Eingabebild betrifft.
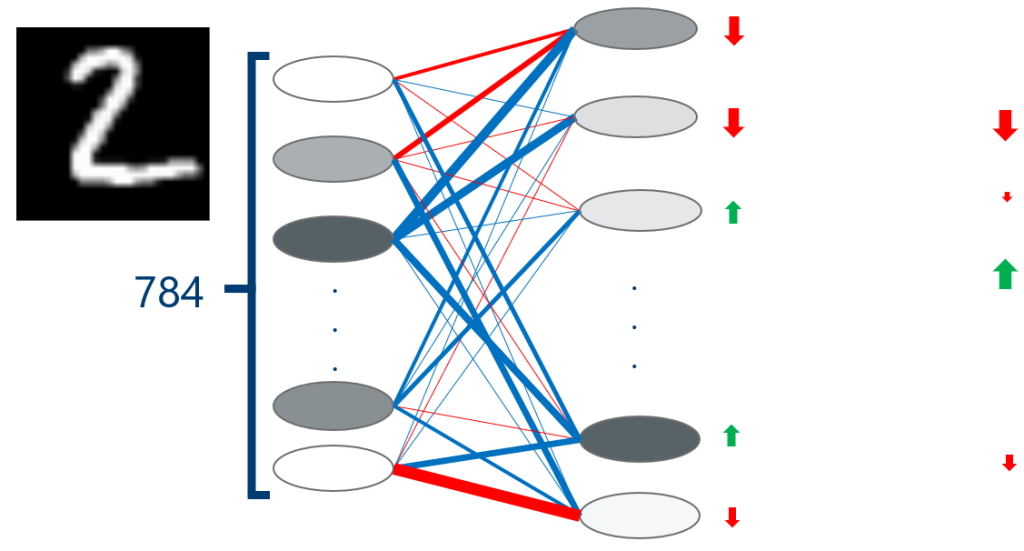
Um das Netzwerk nicht darauf zu trainieren, bei beliebiger Eingabe einfach immer eine 2 auszugeben, können wir diese Berechnung für alle Trainingsdaten durchführen und danach wieder mitteln. Um Rechenaufwand zu sparen, würden wir in der Realität unsere Trainingsdaten in mehrere repräsentative Portionen aufspalten. Im Anschluss passen wir die Gewichte und Biases entsprechend an und evaluieren unseren Gradienten von neuem, so dass sich ein iterativer Lernprozess ergibt.
Fazit
Backpropagation ist ein Algorithmus zur Gradientenberechnung in einem neuronalen Netz. Der Grundgedanke dabei ist es, die notwendigen Berechnungen ausgehend von dem Output Layer Schicht für Schicht nach vorne zu verlagern. In diesem Beitrag haben wir bewusst die Mathematik (fast) außen vorgelassen und stattdessen versucht, eine Intuition dafür zu schaffen, wie der Lernprozess für ein Neuronales Netz ablaufen kann.



