Formale Methoden in der Softwareentwicklung

In Diskussionen mit anderen Softwareentwicklern, insbesondere über Softwaretests, treffe ich häufig auf starken Widerstand, wenn ich das Thema formale Methoden erwähne. Ich sehe mich dabei stets mit Argumenten konfrontiert, die irgendwo zwischen NP-Vollständigkeit, Satz von Rice und Gödelscher Unvollständigkeit fallen. Es sei nicht effizient bis unmöglich. Es ist schon klar, dass sich Softwareentwickler kaum tagelang die Zähne an einem Beweis ausbeißen möchten; und das nur um sicher zu stellen, dass eine einzige Zeile Code genau das richtige Verhalten hat. Wir sind schließlich nicht in der Forschung.

Formale Verifikation, Beweisassistenten

Dennoch finde ich diesen Widerstand nicht unbedingt gerechtfertigt; jeder Softwareentwickler nutzt tagtäglich statische Analysewerkzeuge und weiß diese zu schätzen; dies fängt schon mit der semantischen Vervollständigung einer IDE oder hilfreichen Compilerfehlermeldungen an; Mittel, die heute nicht mehr wegzudenken sind. Darüber hinaus gibt es aber auch Sprachen wie Rust oder haskell; diese rühmen sich mit Eigenschaften wie Speichersicherheit, Typsicherheit oder Seiteneffektfreiheit (und zumindest Rust scheint sich da steigender Beliebtheit zu erfreuen). Man muss also nicht gleich zu einem Beweisassistenten wie Coq, Isabelle, Agda, etc. greifen, um zumindest manche Eigenschaften von Software formal verifiziert zu bekommen.

Es ist selbstverständlich nicht notwendig, machbar oder wünschenswert, jeden Aspekt einer komplexen Software vollständig formal zu spezifizieren und zu verifizieren. Beweise sind schwer und gemäß der Curry-Howard-Korrespondenz sind Beweise gewissermaßen das Gleiche wie Programme. Sie erfordern also genauso ein hohes Maß an Kreativität. Da ist es wirklich etwas viel verlangt, jedes Programm ein zweites Mal, als formalen Beweis, von Entwicklern implementieren zu lassen.

Aber wünschenswerte Eigenschaften und Spezifikationen formal zu verifizieren, kann sehr selektiv geschehen. In der Forschung werden schon seit Jahrzehnten ganze Spektren von Logiken und formalen Sprachen erfunden und analysiert, um in unterschiedlichen Detailgraden, generisch oder Domänen-spezifisch, Äquivalenzen und Erfülltheit von verschiedensten Eigenschaften beweisen zu können. Vor wenigen Jahren hat der Z3 SMT-Solver (Satisfiability Modulo Theories) der Anwendbarkeit und Benutzbarkeit von formaler Verifikation einen gewaltigen Schub verpasst; Z3 ist eines der beeindruckendsten und gleichzeitig wohl am wenigsten bekannten Projekte von Microsoft; ja, selbst Microsoft investiert in die formale Verifikation von Aspekten ihres Betriebssystems. Microsofts SMT-Solver ist inzwischen in Beweisassistenten integriert und hat bindings für gängige Programmiersprachen. Dennoch werden wir vermutlich noch sehr lange darauf warten müssen bis Beweisassistenten in den Alltag eines Softwareentwicklers einziehen werden.

Model Checking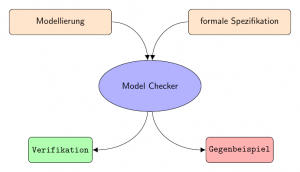

Jedoch gibt es auch noch andere formale Methoden, die nicht von einem Entwickler abverlangen, Beweise zu erfinden. Dies stellt eine deutlich geringere Einstiegshürde dar. Ein teilweise schon in der Industrie eingesetztes Werkzeug ist Model Checking. Model Checker haben nicht nur den Vorteil, dass Beweise vollautomatisiert sind, sondern liefern auch automatisch Gegenbeweise, wenn eine gewünschte Eigenschaft verletzt ist. Dies bedeutet, dass fehlerhafte Zustände oder Verhalten direkt identifiziert werden – also genau das, was man sich auch von einem guten Compiler wünscht. Insbesondere hilfreich sind Model Checker bei Design und Spezifikation von Zustandsmaschinen oder Prozessen; dabei können selbst schwierige Eigenschaften, wie die Abwesenheit von Deadlocks und Livelocks, Liveness, Terminierung, etc. automatisch nachgewiesen werden.

Auf der anderen Seite sind solche Tools natürlich nicht so mächtig wie Beweisassistenten oder Frameworks, die Eigenschaften von (annotiertem) Programmcode verifizieren können. Model Checker kommen aktuell schon in der Hardwareentwicklung zum Einsatz; manche Model Checker bieten sogar Codegenerierung; deshalb denke ich, dass sie auch in der Softwareentwicklung ein mächtiges Werkzeug darstellen könnten. Außerdem bieten sie den gleichen Vorteil wie andere statische Analysemethoden: die Codequalität wird zu einem früheren Zeitpunkt verbessert, was bekannterweise viel Zeit und Geld sparen kann.

Anwendung im Design

Sollte also das nächste Mal das Design eines komplexeren Systems anstehen, würde ich durchaus empfehlen formale Methoden nicht von vornherein zu ignorieren; stattdessen empfehle ich eine Modellierung in einem passenden Model Checker, vielleicht zunächst mit einem niedrigen Detailgrad. Die Einstiegshürde ist schließlich nur das Lernen einer weiteren formalen Sprache (wie UML) und schon kann man wünschenswerte Eigenschaften in Form von formalen Spezifikationen automatisch beweisen lassen. Dabei kann es durchaus hilfreich sein, schon mal was von temporalen Logiken wie LTL oder CTL gehört zu haben – Logiken, die Eigenschaften von Ausführungspfaden von Programmen beschreiben, haben essentiell die gleichen Grundprinzipien, die man schon von den üblichen kontrollflussorientierten Testverfahren kennt.

Der Vorteil, den man dabei gewinnt, ist eine gewaltige Reduktion der Komplexität des nötigen Testaufwandes für die tatsächliche Implementierung. Selbst wenn Codegenerierung nicht zur Verfügung steht, müssen Tests lediglich nachweisen, dass einzelne Zustände sich lokal richtig verhalten. Die Korrektheit des Gesamtsystems folgt aus der Modellierung, deren Korrektheit unser Model Checker beweisen kann. Auch ein agiles Umfeld steht dem Einsatz nicht im Wege. Ein Modell muss nicht erst in einer langen Designphase entwickelt werden und kann jederzeit modifiziert werden. Alle bisher bewiesenen Eigenschaften helfen als Regressions-Beweise. Man kann sogar mit der Formulierung der gewünschten Eigenschaften anfangen – Proof Driven Development sozusagen.